Характерно, что используемое центральными банками ограничение но величине максимального риска на одного заемщика (в виде нормативного отношения совокупной суммы обязательств заемщика по его кредитам к капиталу банка) не связано непосредственным образом с величиной риска невозврата кредита в каждой конкретной сделке, В основу такого нормативно­го регулирования кредитов положено то предположение, что не следует предоставлять слишком большой кредит одному заемщику вне зависимости от уровня его надежности. Подобное регулирование никак не связано с ценообразованием, оно нацеливается на уменьшение суммарного риска.

Таблица 3.4 - Расчет коэффициента суммы выплаты при соответствующим росте невозврата кредита.

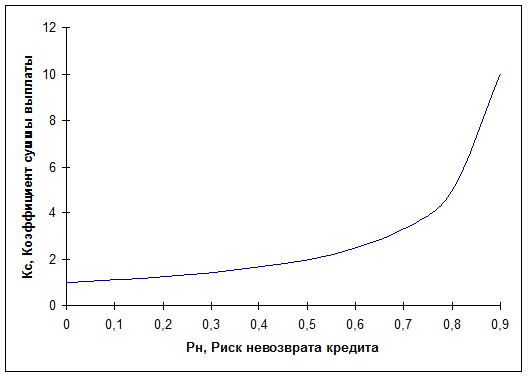
Следующая задача — рассмотрение модели рискового банковского ценообразования, в которой учитывается риск невозврата кредита по всей группе заемщиков. Выше предполагалось: для каждой операции вероятность полного невозврата кредита известна, что дает банку возможность регулировать процентную ставку в зависимости от уровня риска. Однако в условиях массового предоставления кредита и отсутствия возможности изучения каждого клиента в отдельности коммерческий банк вынужден ориентироваться на некий средний уровень ожидаемого риска, распространяя этот уровень на все проводимые операции и на всех клиентов. При такой ценовой стратегии банк повышает цену кредита в виде ссудного процента на одну и туже величину, отражающую средний уровень риска, т. е. на среднюю по всем сделкам величину его вероятности Рн.

Рисунок 3.3– Зависимость увеличения суммы выплат от вероятности невозвращения кредита заемщиком

Математическая модель ценообразования в виде формулы относительной ставки кредитного процента в этом случае мало чем отличается от зависимости (4) и может быть представлена в следующем виде:

= + Рн/ (1-Рн-q)* (1 +). (10)

Принципиальная особенность данной модели (здесь q –показатель изменения риска) состоит в том, что в ней вероятность невозвращения кредита Рн относится ко всему портфелю кредитов банка. Поэтому значения Рн тут обычно существенно ниже, чем для сделок с высокой степенью риска, и рисковая ставка может не отличаться значительно от безрисковой ставки .

Поскольку в определенных сделках (для отдельных заемщиков) риск ниже среднего, В формулу (10) введен показатель изменения рис «премией за портфельный риск». Этот показатель характеризует, каким образом и в какой степени сделка, для которой вычисляется процентная ставка , образом более низким риском в сравнении с уровнем риска, исчисленным для всего портфеля кредитов банка. Если риск повышается, q > 0, а если понижается, q < 0 (величина q принимается в доле от вероятности Рн).

Хотя в названных обстоятельствах банковский кредитный процент может расти в меньшей мере, чем он повышается по отношению к весьма рискованным сделкам, подобная ценовая стратегия несовершенна. По сути она переносит компенсацию риска, порождаемого отдельными ненадежными заемщиками, на всех остальных заемщиков, а значит, способна отпугнуть их (что понятно, крайне нежелательно и ведет к повышению банковского риска). К тому же при таком способе ценового поведения высоки шансы проиграть соревнование с конкурентами. Иными словами, в условиях кредитного риска необходим избирательный подход в ценообразовании. Этого рода подход и реализуется чаще всего коммерческими банками, но без использования моделей ценообразования.

Более сложны эти модели в условиях кредитного риска, связанного с опасностью неполного возврата банковского кредита. В общем случае при такой ситуации приходится иметь дело со спектром вероятностей. Речь идет о кривой вероятностей Р(а) невозврата, характеризующей зависимость каждой доли вероятности от доли а, которую составляет невозвращенный кредит в общей сумме кредита. Практически же приходится рассматривать не кривую Р(а), а столбиковую диаграмму частот (гистограмму). Иначе говоря, весь диапазон долей невозврата делится на n частей, любой из которых соответствует своя доля (а1, а2... ап), А каждой доле соответствует вероятность (относительная частота) Рi того, что такая доля кредита не будет возращена.

Подобное разделение возможно как применительно к отдельной кредитной сделке, так и ко всей совокупности сделок, осуществляемых банком в течение определенного периода времени. Не исключена и ситуация, при которой для каждого клиента банка может быть установлена кривая распределения вероятностей (относительных частот) невозврата определенных долей получаемых им кредитов банка,

Итак, пусть известно, что каждому i-ому интервалу, характеризуемому долей аi кредитов, выданных банком, соответствует вероятность Рi невозврата этой доли. Тогда общий невозврат в данной сделке или во всех сделках за определенный период времени составит

Р i аi (1 + )* К, где К — общая величина кредита, — относительная ставка процента банковского кредита. Сумма возвращенного банку кредита соответственно равна (1- Р i аi) (1 + )* К.

Чтобы компенсировать потери, обусловленные неполным возвращением кредита, банк вынужден устанавливать относительную ставку кредитного процента , удовлетворяющую условию равенства процентных поступлений при наличии и отсутствии риска. Речь идет о следующем соотношении;

(1- Р i аi) (1 + )* К.= (1+)*К (11)

Где — относительная ставка процента при отсутствии риска

Отсюда вытекает, что в условиях риска частичного невозврата кредита, банк должен установить относительную ставку кредитного процента, выражаемую зависимостью

=(1+) /(1- Р i аi)-1=(+Р i аi)/(1-Р i аi) (12)

Полученное выражение представляет обобщение формулы (3), обоснованной применительно к условиям риска полного невозврата кредита.

Введя среднее значение Pсp вероятности невозврата кредита (математическое ожидание невозврата), определяемое соотношением

Рср=Р i аi (13)

Можно выявить зависимость для относительной процентной ставки в условиях риска неполного возврата кредита:

=(+Рср)/(1-Рср) (14)

Полученная зависимость воплощает математическую модель ценообразования в условиях риска неполного возврата кредита, ибо величина представляет основной ценовой параметр.