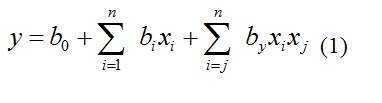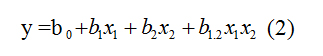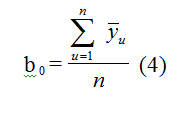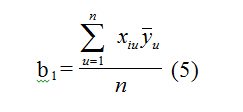|
Страница 6 из 13
По многочисленным ранее проведенным исследованиям установлено, что на потери зерна наибольшее влияние оказывают два фактора: - угловая скорость очесывающего барабана и H - величина погружения очесывающих пальцев в стеблевую массу.
3.1.3. 3 этап. Выбор математической модели.
Когда неизвестен механизм протекания процесса в «черном ящике» аналитическое выражение функции отклика также неизвестно. Поэтому описывают функцию отклика уравнением регрессии вида:
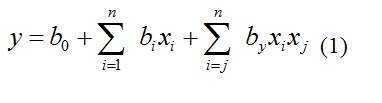
где x и x - значения факторов;
b - свободный член, равный выходу при x = 0;
b -коэффициент регрессии соответствующих факторов на изучаемый объект;
b -коэффициент регрессии соответствующих факторов двойного взаимодействия.
Для нашего примера с двумя факторами x = и x уравнение регрессии будет иметь вид:
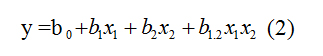
Для трех факторов x x x :
Y= b0 +b1 x1 +b2 x2 +b3 x3 +b1,2 x1x2+b1,3x1x3+b2,3x2x3+b1,2,3x1x2x3 (3)
Коэффициенты уравнения регрессии рассчитывают по результатам эксперимента. Величина коэффициентов регрессии и знак характеризуют данный фактор, его влияние на параметр оптимизации.
3.1.4. 4 этап. Составление схемы проведения опытов.
При планировании многофакторного эксперимента могут применяться следующие методы:
а) полный факторный эксперимент (ПФЭ);
б) дробный факторный эксперимент (ДФЭ);
в) симплексный метод;
г) отсеивающие эксперименты и др.
При планировании используем метод полного факторного эксперимента (ПФЭ) и приводим построение плана ПФЭ.
При составлении плана эксперимента назначают уровни варьирования факторов. Обычно принимают 2 уровня и обозначают их «+1» и «-1».
Таблица 1. Уровни варьирования факторов
|
№ п/п
|
Факторы
|
Обозначения
|
Уровни факторов
|
|
— 1
|
+ 1
|
|
1
|
Угловая скорость, 1/с
|
х
|
|
|
|
2
|
Величина погружения, м
|
х
|
|
|
Комбинации условий эксперимента при 3-х уровнях определяются
показательной функцией N = 2 , где n - количество факторов.
Эти комбинации условий (количество опытов) можно представить в виде таблицы сочетаний разных уровней факторов, упорядоченных по столбцам. Такая таблица называется матрицей планирования. Строки матрицы соответствуют различным опытам, а столбцы – значениям факторов.
Таблица 2. – Матрица планирования двухфакторного эксперимента типа N = 22
|
Номер
опыта
|
х0
|
х1
|
х2
|
х1х2
|
Вектор выхода y
|
|
Повторности
|
Ср. значение
|
|
у1
|
у2
|
у3
|
уu (уср)
|
|
1
|
+
|
-
|
-
|
+
|
у11
|
у12
|
у13
|
уср1
|
|
2
|
+
|
+
|
-
|
-
|
у21
|
у22
|
у23
|
уср2
|
|
3
|
+
|
-
|
+
|
-
|
у31
|
у32
|
у33
|
уср. 3
|
|
4
|
+
|
+
|
+
|
+
|
у41
|
у42
|
у43
|
уср4
|
В матрице планирования в 1-ом столбце записываются номера опытов, которые необходимо рандомизировать (ввести случайность в последовательность их выполнения).
2-й столбец представляет собой «фиктивную» переменную x .
3-4-й столбцы образуют собственно планирование.
5-й - показывает возможность взаимодействия факторов x и x .
В 6-8 столбцах вносятся результаты опытов по каждой повторности.
Количество повторностей принимают в зависимости от заданной точности опытов. Обычно 3 повторности. В последнем столбце вносятся средние значения повторностей опытов (количество повторностей определяется с учетом требуемой надежности опыта).
3.1.4. 5 этап. Проведение эксперимента.
Согласно составленной рабочей матрице (с учетом рандомизации опытов) проводят эксперименты с 3-х кратной повторностью. Значение параметра оптимизации (P = Y - потери зерна), полученного в каждом опыте записываются в рабочую матрицу.
3.1.5. 6 этап. Обработка результатов эксперимента с использованием статистических методов и регрессионного анализа.
а) Расчет коэффициентов регрессии математической модели:
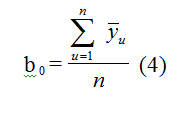
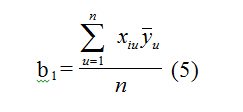
По формуле (5) определяются коэффициенты b , b , b и b уравнений регрессий
б) Подставляются полученные значения коэффициентов регрессии в уравнение (2):
у = b0 + b1x1 + b2x2 + b1,2x1x2
|