| Полный конспект лекции по топографии 23 лекции. |
 |
 |
| Добавил(а) Administrator |
| 15.02.11 18:53 |
|
Страница 20 из 31
С левой стороны плана помещают описание смежных земель, (например от А до В – с землями совхоза «Пригородный» и т.д.).
Внизу под планом указывают масштаб плана, вычерчивают линейный или поперечный масштаб, справа указывают фамилию исполнителя съемки и составителя плана, а слева фамилии принимавших и проверявших все полевые и камеральные документы по съемке и составлению плана с личными подписями всех этих лиц. Лекция 14. Способы определения площадей 1.Способы определения площадей. 2.Аналитический способ. 3.Графический (геометрический) способ. 4.Определение площадей палетками. 5.Механичекий способ. 1. В зависимости от хозяйственного значения участков и контуров, их размеров, формы, наличия или отсутствия планов и карт, естественноисторических условий местности. а) Аналитический – площади вычисляют по результатам измерений линий и углов на местности с применением формул геометрии, тригонометрии и аналитической геометрии. Например, при учете площадей, занятых строениями, усадьбами, площадей вспашки, посева, при отводе мелких участков их разбивают на простейшие геометрические фигуры, преимущественно треугольники, прямоугольники, реже трапеции и площади участков определяют как суммы площадей отдельных фигур, вычисляемых по отдельным элементам (высотам и основаниям) по общеизвестным формулам геометрии. При учете вспашки, посева, уборки урожая, площади определяют также по длине маршрута агрегата и ширине его захвата. Площади больших участков, целых землепользований вычисляют по результатам измерений линий и углов на местности (при помощи формулы тригонометрии) или по их функциям – приращениям координат и координатам вершин полигона. б) Графический – площади вычисляют по результатам измерений линий на плане или карте, когда участок, изображенный на плане разбивают на простейшие геометрические фигуры, преимущественно треугольники, реже прямоугольники и трапеции. В каждой фигуре измеряют высоту и основание, но которым вычисляют площадь: сумма площадей фигур дает площадь участка (подробнее с картинками, удвоенная площадь). К графическому способу относят определение площади палетками. 2. Аналитический способ. Вычисление площади полигона по координатам его вершин. Площадь полигона 1-2-3-4-5, которую обозначим через Р, можно представить как разность площадей фигур А-1-2-3-4-В и А-1-5-4-В, при этом площадь каждой из этих фигур может быть представлена как сумма площадей трапеций с основаниями х и высотами у2-у1; у3-у2 и т.д. т.е. Р=плошА-1-2-3-4-В – площА-1-5-4-В= =1/2(х1+х2)(у2-у1)+1/2(х2+х3)(у3-у2)+1/2(х3+х 4)(у4-у3)-1/2(х4+х5)(у4-у5)-1/2(х5+х1)(у5 -у1) в двух последних членах можно изменить знаки и все выражение записать так: 2Р=(х1+х2)(у2-у1)+(х2+х3)(у3-у2)+(х3-х4 )(у4-у3)+(х4+х5)(у5-у4)+(х5+х1)(у1-у5) в полученном выражении наблюдается закономерность, что удвоенная площадь полигона равна сумме стольких произведений, сколько вершин имеет полигон, при этом в каждом произведении один сомножитель есть сумма абсцисс двух соседних точек с номерами п и п+1; а другой сомножитель – разность ординат этих точек с номерами п+1 и п. Это дает возможность сокращенно написать формулу для любого п-угольника
Аналогично в выражении Результаты вычислений по формуле 3 и 4 можно контролировать разности (суммы их =0). Перед вычислением площади, значения координат можно округлить до 0,1 м, а если площадь полигона более 200 га, то до 1м, т.к. это округление упрощает вычисления без заметного снижения точности результатов вычисления площади. Площадь, выходящую за пределы полигона, т.е. часть её между сторонами полигона и живым урочищем определяют как сумму площадей трапеций и треугольников, образованных сторонами полигона и перпендикуляров, длины которых получены из измерений на местности и записаны в абрисе. Некоторые элементы треугольников определяют по плану. Площади отдельных треугольников определяется по известной формуле тригонометрии Определение площадей палетками Квадратные палетки(до 2 см2 на плане) Параллельные палетки
Лекция 15 Механический способ определения площадей 1.Полярный планиметр и его теория. 2.Цена деления полярного планиметра и способы ее строения. 3.Испытания и поверки планиметра. 1.Планиметром называется механический пробор, дающий возможность путем обвода плоской фигуры любой формы определить ее площадь. Они бывают самых разнообразных систем от очень сложных до самых простых. Планиметры делятся на линейные и полярные. Наиболее распространены полярные планиметры состоят из двух рычагов (обводного R и полюсного R0), соединенных шарниром в т.а. (показать полярный планиметр и его устройство, подробно рассказать, как им пользоваться). Планиметр компенсационный с переменным обводным рычагом. Компенсационным планиметром можно измерять площадь двумя полуприёмами – полюс слева, полюс справа. Когда мы работаем с планиметром, то видим, что счетный ролик вращается в прямом и обратном направлении, но в итоге мы получаем площадь(в единицах планиметра). Как это объяснить? Для этого надо проникнуть в теорию полярного планиметра. Изобразим схематически полярный планиметр. Здесь Кроме того, обозначим через Для правильной работы планиметра требуется выполнение основного геометрического условия – на направление рифельных штрихов на ободке счетного ролика должно быть параллельно оси обводного рычага, т.е. линии, проходящей через т.т.
|
| Последнее обновление 15.02.11 19:31 |
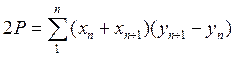 из этой формулы можно получить много других формул, выражающих площадь полигона через приращение координат и через координаты вершин. Выведем 3 наиболее известные формулы вычисления площади полигона по координатам его вершин. Для этого раскроем скобки
из этой формулы можно получить много других формул, выражающих площадь полигона через приращение координат и через координаты вершин. Выведем 3 наиболее известные формулы вычисления площади полигона по координатам его вершин. Для этого раскроем скобки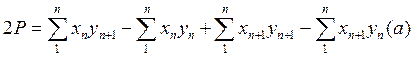 , но в этом выражении
, но в этом выражении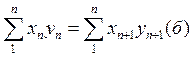 получим что обе части этого равенства представляют сумму произведений абсциссы каждой точки на ординату этой же точки. Тогда вместо
получим что обе части этого равенства представляют сумму произведений абсциссы каждой точки на ординату этой же точки. Тогда вместо 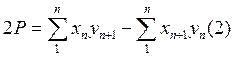 , теперь в этой формуле можно произвести замену
, теперь в этой формуле можно произвести замену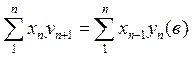 , потому что обе части этого равенства представляют суммы произведений абсциссы каждой точки на ординату последующей точки учитывая
, потому что обе части этого равенства представляют суммы произведений абсциссы каждой точки на ординату последующей точки учитывая 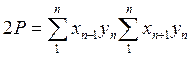 , или вынесем за скобки
, или вынесем за скобки 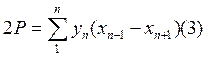 следовательно,
следовательно, 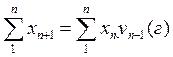 и с учетом
и с учетом 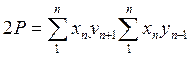 , или вынося за скобки
, или вынося за скобки 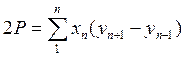 , т.е. удвоенная площадь полигона равна сумме произведений каждой абсциссы на разность ординат последующей и предыдущей точек.
, т.е. удвоенная площадь полигона равна сумме произведений каждой абсциссы на разность ординат последующей и предыдущей точек.


