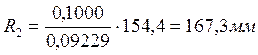|
Страница 21 из 31
Плоскость счетного ролика должна быть перпендикулярна к оси обводного рычага.
При обводе фигуры обводной рычаг, а вместе с ним и счетный ролик имеют 4 вида движения.
1)Если счетный ролик движется в своей плоскости перпендикулярно к направлению рифельных штрихов и оси обводного рычага, то он будет вращаться и обернется на дугу 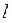 , соответствующую пройденному пути , соответствующую пройденному пути 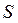 . .
2)Если счетный ролик движется по направлению рифельных штрихов и оси обводненного рычага перпендикулярного к своей плоскости, то он не будет вращаться, а будет только скользить, и длина дуги, на которую он обернется, будет равна нулю независимо от пройденного пути.
3)Если счетный ролик движется под углом 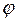 к направлению рифельных штрихов, а следовательно под углом к направлению рифельных штрихов, а следовательно под углом 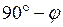 к своей плоскости, то он будет и вращаться и скользить, и пройдя путь S, обернется на дугу к своей плоскости, то он будет и вращаться и скользить, и пройдя путь S, обернется на дугу 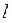 , представляющую собой катет прямоугольного треугольника, у которого гипотенуза равна S, при этом , представляющую собой катет прямоугольного треугольника, у которого гипотенуза равна S, при этом 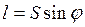
4)При вращении обводного рычага вокруг т. 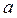 (оси вращения рычагов), счетный ролик будет вращаться и скользить, пройдет путь по дуге (оси вращения рычагов), счетный ролик будет вращаться и скользить, пройдет путь по дуге 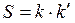 и обернется на дугу и обернется на дугу 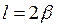 независимо от положения счетного ролика в своей плоскости. Если т. независимо от положения счетного ролика в своей плоскости. Если т. 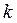 находится на оси обводного рычага, когда находится на оси обводного рычага, когда 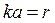 , то в этом случае счетный ролик будет только вращаться и обернется на ту же дугу , то в этом случае счетный ролик будет только вращаться и обернется на ту же дугу 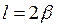 . .
Выведем формулы, по которым определяют площади обводимых фигур. Для обвода большой фигуры планиметр устанавливают полюсом О внутри ее. Обводный индекс 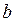 ставят на контур фигуры и берут отсчет по счетному ролику. Пусть при обводе фигуры обводный индекс прошел по контуру очень малое расстояние из т. ставят на контур фигуры и берут отсчет по счетному ролику. Пусть при обводе фигуры обводный индекс прошел по контуру очень малое расстояние из т. 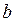 в т. в т. 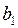 , вследствие чего планиметр двигался над площадью , вследствие чего планиметр двигался над площадью  . Можно представить, что обводный индекс прошел еще малое расстояние . Можно представить, что обводный индекс прошел еще малое расстояние 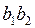 , а планиметр двигался над площадью , а планиметр двигался над площадью 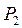 , затем над площадью , затем над площадью 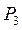 и т.д. наконец, обводной индекс пришел в т. и т.д. наконец, обводной индекс пришел в т. 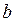 , а планиметр прошел над всей площадью обведенный фигуры , а планиметр прошел над всей площадью обведенный фигуры 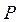 , представляющей собой сумму большого числа отдельных малых площадей , представляющей собой сумму большого числа отдельных малых площадей 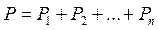 . .
Рассмотрим отдельно площадь 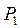 . Для разбивки ее на простейшие геометрические фигуры представим, что сначала обводной рычаг перемещался параллельно самому себе и из положения . Для разбивки ее на простейшие геометрические фигуры представим, что сначала обводной рычаг перемещался параллельно самому себе и из положения 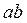 пришел в положение пришел в положение 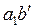 , а затем повернулся около т. , а затем повернулся около т. 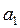 и пришел в положение и пришел в положение  . Тогда площадь . Тогда площадь 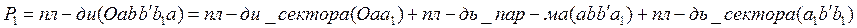 , или , или 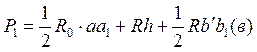 , по дуга , по дуга 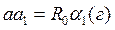 , а дуга , а дуга 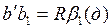 . Здесь и далее углы . Здесь и далее углы 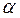 и и 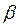 выражаем для удобства в радианной мере. Высоту выражаем для удобства в радианной мере. Высоту 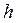 параллелограмма выразим через дугу параллелограмма выразим через дугу 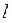 , на которую обернется счетный ролик при переходе обводного рычага из положения , на которую обернется счетный ролик при переходе обводного рычага из положения 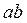 в положения в положения 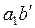 счетный ролик и выражался и скользил, а пройдя путь по дуге счетный ролик и выражался и скользил, а пройдя путь по дуге 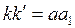 , обернулся на дугу , обернулся на дугу 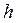 (согласно рисунку). (согласно рисунку).
Когда свободный рычаг вращался около точки 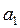 и переходил из положения и переходил из положения 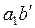 в положение в положение  , счетный ролик только вращался в обратную сторону, прошел путь по дуге , счетный ролик только вращался в обратную сторону, прошел путь по дуге 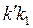 и обернулся на эту дугу, вследствие чего и обернулся на эту дугу, вследствие чего 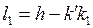 , но , но 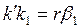 , поэтому , поэтому 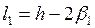 и и 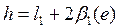 . Подставив значения . Подставив значения 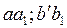 и и  из из 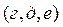 в выражение в выражение 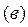 , получим: , получим: 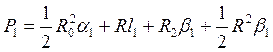 . Малые площади . Малые площади  и др., выразится аналогичными формулами: и др., выразится аналогичными формулами:
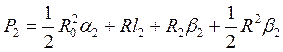 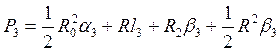 и т.д. Сложив их, мы получим: и т.д. Сложив их, мы получим: 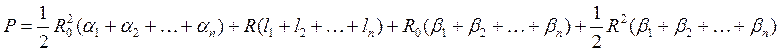 , по , по 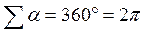 (рычаг планиметра обернулся на полную окружность). Углы (рычаг планиметра обернулся на полную окружность). Углы 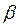 тоже в сумме составляют тоже в сумме составляют 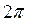 . Кроме того, сумма дуг . Кроме того, сумма дуг 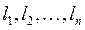 составит дугу, на которую повернется счетный ролик, когда обводной индекс пройдет по всему контуру фигуры и пройдет в исходную т. составит дугу, на которую повернется счетный ролик, когда обводной индекс пройдет по всему контуру фигуры и пройдет в исходную т. 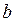 обозначим ее через обозначим ее через 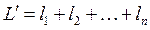 . С учетом вышесказанного, перепишем там . С учетом вышесказанного, перепишем там 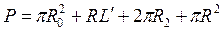 или или 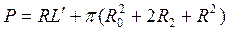 . .
Все величины, входящие во второе слагаемое этой формулы, постоянны (при установке планиметра на определяемое значение R) поэтому обозначим его через С т.е. 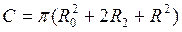 . Величина С называется постоянным числом планиметра, отсюда: . Величина С называется постоянным числом планиметра, отсюда: 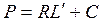 . Теперь согласно формулы . Теперь согласно формулы 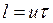 выразим выразим 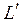 через деление планиметра через деление планиметра 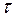 и число делений и число делений 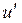 , на которое обернется счетный ролик при обводе всей фигуры т.е. , на которое обернется счетный ролик при обводе всей фигуры т.е. 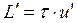 , отсюда , отсюда 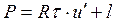 , но величины , но величины 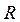 и и 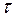 постоянны и их произведение постоянны и их произведение 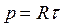 , есть величина постоянная (при данной длина обводного рычага) и называется ценой деления планиметра. Число делений , есть величина постоянная (при данной длина обводного рычага) и называется ценой деления планиметра. Число делений 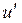 , на которое обернется счетный ролик, когда обводной индекс пройдет по всему контуру фигуры (по ходу часовой стрелки) получается как разность отсчетов после обвода , на которое обернется счетный ролик, когда обводной индекс пройдет по всему контуру фигуры (по ходу часовой стрелки) получается как разность отсчетов после обвода 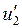 и до обода и до обода 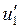 , т.е. , т.е. 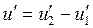 . .
Постоянное число планиметра С есть площадь, которую можно выразить через цену деления планиметра 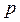 и число делений и число делений 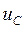 , заключенной в площади С, т.е. , заключенной в площади С, т.е.  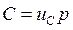 , таким образом заключение площади примет вид , таким образом заключение площади примет вид 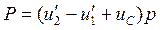 (эта формула для определения площади, когда полюс внутри фигуры). Эта формула показывает, что для определения площади нужно обверти фигуру по ходу часовой стрелки, чтобы получить (эта формула для определения площади, когда полюс внутри фигуры). Эта формула показывает, что для определения площади нужно обверти фигуру по ходу часовой стрелки, чтобы получить 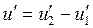 , кроме того надо знать 2-е постоянные величины , кроме того надо знать 2-е постоянные величины 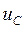 и и 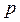 . .
О способе их определения будет сказано дальше. Для определения площади небольшой фигуры полюс О устанавливают вне ее.
Здесь формула определения площади после аналогичных вычислений получается в виде 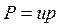 , т.е. она показывает, что для определения площадь нужно обвести фигуру по ходу часовой стрелки, найти , т.е. она показывает, что для определения площадь нужно обвести фигуру по ходу часовой стрелки, найти 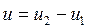 , и знать одну постоянную величину , и знать одну постоянную величину 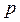 (цену деления планиметра). (цену деления планиметра).
2.Цена деления полярного планиметра и способы ее определения
Формула 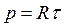 называют, что цена называют, что цена 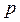 деления планиметра равна произведению длины обводного рычага деления планиметра равна произведению длины обводного рычага 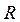 на длину на длину 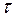 одного деления планиметра. одного деления планиметра.
Геометрически цена деления планиметра представляет площадь прямоугольника с основанием, равным длине обводного рычага 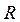 , и высотой, равной одному делению планиметра , и высотой, равной одному делению планиметра 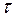 . При определении площадей земельных участков обычно пользуются не абсолютной ценой деления, определяется этой формулой, а относительной, когда . При определении площадей земельных участков обычно пользуются не абсолютной ценой деления, определяется этой формулой, а относительной, когда 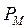 - выражается в га или м2 на местности, т.е. с учетом масштаба плана. - выражается в га или м2 на местности, т.е. с учетом масштаба плана.
Для этого величины 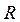 и и 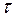 умножаем на знаменатель масштаба плана умножаем на знаменатель масштаба плана 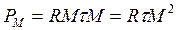 . Например, при . Например, при 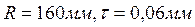 , масштаб 1:10 000. , масштаб 1:10 000. 
Величину Р можно было бы вычислить по результатам 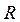 и и 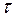 , но величина , но величина 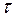 очень мала, которую измерить до четвертой значащей цифры очень трудно. Поэтому цену деления планиметра определяют по формуле очень мала, которую измерить до четвертой значащей цифры очень трудно. Поэтому цену деления планиметра определяют по формуле 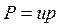 . Для определения . Для определения 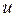 фигуру, площадь которой известна обводят при положении полюса вне ее(например квадрат координатной сетки). фигуру, площадь которой известна обводят при положении полюса вне ее(например квадрат координатной сетки). 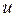 будет определяться как разность конечного и начального отсчета. будет определяться как разность конечного и начального отсчета. 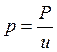 обычно эту процедуру повторяют несколько раз при двух положениях полюса и берут среднее значение обычно эту процедуру повторяют несколько раз при двух положениях полюса и берут среднее значение  . При этом угол между рычагами должен быть не менее . При этом угол между рычагами должен быть не менее 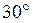 и не более и не более 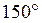 . Записи и вычисления заносят в таблицы(конкретнее на практических занятиях). Цену деления вычисляют до четырех значащих цифр. . Записи и вычисления заносят в таблицы(конкретнее на практических занятиях). Цену деления вычисляют до четырех значащих цифр.
Удобно пользоваться планиметром, если цена деления круглое число. Чтобы этого добиться, надо изменить длину обводного рычага, т.е. 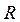 . Если у нас цена деления . Если у нас цена деления 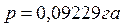 , для масштаба 1:10 000, при длине обводного рычага , для масштаба 1:10 000, при длине обводного рычага 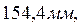 то чтобы получить то чтобы получить 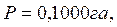 можно рассчитать длину R2. можно рассчитать длину R2.
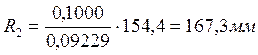
3.Испытания и поверки планиметра
При осмотре планиметра к нему должны быть предоставлены следующие требования:
1).Счетный ролик должен свободно вращаться на оси, не задевая за верньер и не иметь шатание в подшипниках (должен свободно вращаться 3-4 секунды). Между счетным роликом и верньером должен быть зазор толщиной с тонкий лист бумаги. Регулировка ролика осуществляется с помощью винтов, держащих подшипник.
2).Поверхность верньера должна быть продолжением поверхности ролика.
3).Деление на ролике (цилиндрической поверхности) и верньере должны быть правильными. Для этого последовательно совмещают начальный штрих верньера со штрихом на ролике и смотрят, совместился ли штрих верньера с одним из штрихов ролика. Потом повторяют этот процесс со следующим штрихом ролика и т.д.
|


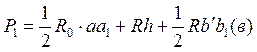 , по дуга
, по дуга 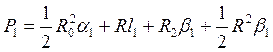 . Малые площади
. Малые площади 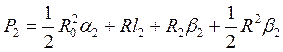
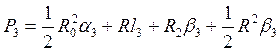 и т.д. Сложив их, мы получим:
и т.д. Сложив их, мы получим: 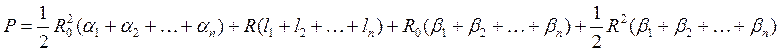 , по
, по 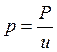 обычно эту процедуру повторяют несколько раз при двух положениях полюса и берут среднее значение
обычно эту процедуру повторяют несколько раз при двух положениях полюса и берут среднее значение