| Полный конспект лекции по топографии 23 лекции. |
 |
 |
| Добавил(а) Administrator |
| 15.02.11 18:53 |
|
Страница 30 из 31
Каждый из этих видов может служить самостоятельной геодезической сетью для мензульной съемки, однако на больших площадях геометрическая сеть и мензульные ходы опираются на пункты триангуляции, полигонометрии и теодолитных ходов.
Высоты пунктов определяют положением ходов геометрического нивелирования или тригонометрического нивелированием. 2.Геометрическую сеть представляет собой систему треугольников. Но от триангуляции она отличается тем, что углы в треугольниках не измеряют, а положение пунктов геометрической сети получают на планшете графически прямой или боковой засечкой. Геометрическая сеть, как съемочное обоснование обычно строят для сгущения геодезической сети, когда имеющиеся пункты триангуляции, полигонометрии и теодолитных ходов расположены редко и не обеспечивают необходимую густоту для съемки местности. Например для съемки масштаба 1:10 000 нужно, на 1 км 2 был хотя бы один пункт любого вида геодезической сети. Длины сторон треугольника геометрической сети примерно занимают 1/10 знаменателя численного масштаба, выраженную в метрах. Поэтому при построении сети в масштабе 1:10 000 длина стороны треугольника геометрической сети примерно равна 1 км, в масштабе 1:5 000 – 0,5км; в масштабе 1:2 000 и крупнее геометрическую сеть обычно не строят. Сгущение геодезической сети пунктами геометрической сети выгодно в том отношении, что их положение на плане (планшете) определяют графически (методом засечек), а следовательно, не возникает необходимость выполнять вычислительные расчеты, как, например, ………….., кроме этого засечки пунктов геометрической сети можно производить одновременно со съемкой ситуации и рельефа с точек уже имеющейся сети. На рисунке точки между пунктами «г. Пригородный» и «Белое» проложен теодолитно-нивелирный ход по т. 1, 2 и 3. Точки 5 и 6 являются пунктами геометрической сети, положение которых нужно определить. Положение этих пунктов можно определить следующим образом. Мензулу устанавливают в пункте «г. Пригородный», ориентируют на точку теодолитного хода 1, визируют на т. 5, прочерчивают направление на планшете и вдоль направления подписывают «г. Пригородный»-т.5. Переходят с мензулой на т.1, ориентируют планшет на пункт «г. Пригородный», проверяют ориентир на т. 2, визируют на т.5. Пересечение двух направлений дает положение т.5 на планшете и т.д. При построении геометрической сети необходимо соблюдать следующие правила: - в пункты геометрической сети необходимо включать постоянные предметы местности (шпили башен, антенны, трубы и пр.). Это важно: 1) Потому, что пересечение нескольких направлений в одной точке при засечках постоянных предметов местности свидетельствует о правильности построения геометрической сети. 2) Постоянные предметы, видимые на дальние расстояния дают возможность ориентировать на планшет по длинным линиям. 3) Постоянные предметы – более надежные и долговечные знаки геометрической сети. - пункты должны располагаться на возвышенных местах и каждый пункт мог быть получен прямыми засечками не менее чем с трех точек, а углы в засечках были не менее - планшет нужно центрировать с такой точностью, чтобы погрешность направления не получалась более - планшет нужно всегда ориентировать по наиболее удаленной точке. Если такой возможности нет, то направления на планшете удлиняют; - ориентируют планшет и проводят направления на определенные пункты при одном положении ВК (обычно при КЛ), чтобы ослабить влияние остатков коллимационной ошибки. Измерение углов наклона геометрической сети . После проведения направлений на засекаемые пункты измеряют углы наклона на них, если высоты пунктов определяют методом тригонометрического нивелирования; при этом не требуется ни точного ориентирования планшета, ни точного приведения его в горизонтальное положение. Углы наклона измеряют по заранее составленной программе наблюдений. Этой программой предусматривается контроль вычисления превышений в прямом и обратном направлениях, например с т.5 на 6 и с т.6 на т.5. Так же программа наблюдений составляется так, чтобы была обеспечена связь с пунктами, высоты которых получены, например, из геометрического нивелирования, а направления, по которым измеряют углы наклона, образовали бы треугольники. Следует иметь в виду что превышения более точно передаются по коротким сторонам, чем по длинным. Углы наклона измеряют полным приемом – при обоих положениях ВК и вычисляют МО. О правильности визирования на точки, приведения пузырька уровня при ВК на середину, а также о правильности отсчетов свидетельствует постоянство МО. МО считается постоянным, если расхождение его значений на одной и той же станции не превышает уровенной средней погрешности измерения угла наклона ( Визирование должно быть на то же место знака, до которого считается его высота Перед измерением Все данные записывают в топографический журнал. 3.Вычисление и увязка превышений между пунктами геометрической сети. Вычисление высот. Превышение вычисляют по формуле
По тем сторонам геометрической сети, по которым превышение определяется дважды, т.е. прямое и обратное, вычисляют среднее. Вычисляют среднее
Для увязки превышений их средние значения выписывают на схему со знаком, соответствующим направлению, показанному стрелкой. Около линий геометрической сети вписывают расстояние между пунктами. Наиболее простым способом сравнения невязок в смежных полигонах (треугольниках). Для этого вычисляют невязки по каждому полигону Допустимую невязку определяют
Для треугольника Принцип сравнения невязок состоит в следующем (стр. 299). Контроль сумма увязанных превышений в каждом полигоне равна 0. Если высота одного из пунктов геометрической сети исходная, то высоты всех остальных пунктов вычисляют 4.Определение положения переходных точек. При съемке в масштабе 1:10 000 расстояние от станции до съемочных точек не допускаются более 250-300м. Способы: а) полярный; б) прямая засечка; в) боковая засечка; г) по створу; д) определение четвертой точки по трем данным – обратная засечка (задача Патенота). Наиболее простой – полярный. 5.Графическое решение задачи Патенота. Сущность: определить положение точки по способу прямой или боковой засечки возможно не менее чем по двум пунктам и двух станций. Задача Патенота решается по трем пунктам и с одной станции в той точке, положение которой определяется. а) аналитический способ б) графический способ На планшете
|
| Последнее обновление 15.02.11 19:31 |
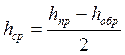 , если расхождение между ними допустимо (
, если расхождение между ними допустимо ( 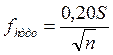 , м, где S – периметр полигона в км, n – число сторон полигона.
, м, где S – периметр полигона в км, n – число сторон полигона.


