| Полный конспект лекции по топографии 23 лекции. |
 |
 |
| Добавил(а) Administrator | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 15.02.11 18:53 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Страница 18 из 31
3. В графу 4 по направлению хода, как указано стрелками вписывают исходные дирекционные углы исходных линий 8-1 и 4-3, взятые из ведомости координат замкнутого хода, причем для линии 4-3 взят обратный дирекционный угол, так как в ведомости координат вычислен дирекционный угол линии 3-4.
4.Увязывают углы. Угловую невязку вычисляют по формуле
в общем виде Но в теодолитном ходе это равенство будет получено только в том случае, если углы
Следовательно, дирекционный угол конечной линии равен дирекционному углу начальной (исходной) линии + сумма левых углов хода - На этом основании В нашем примере а угловая невязка Допустимость невязки определяется в зависимости от числа углов хода, включая примычные, и от того как получены исходные дирекционные углы. Если они получены астрономическим путем или это дирекционные углы сторон геодезической сети высших классов, когда их точность достаточно высока и погрешности почти не влияют на угловую невязку хода, то допустимость угловой невязки можно определить по формуле Если же теодолитный ход опирается на дирекционные углы ранее проложенных теодолитных ходов, то на угловую невязку хода, помимо погрешностей измерения углов, влияют погрешности этих (исходных) дирекционных углов, и допустимость угловой невязки определяется по формуле В этой формуле 5.Вычисляют дирекционные углы, а затем румбы сторон хода так же, как и в полигоне. Контролем правильности увязки углов и вычисления дирекционных углов служит получение исходного дирекционного угла конечной линии. 6.Вычисляют горизонтальное проложение линии хода. 7.Вычисляют приращение координат так же как и в полигоне. 8.Увязывают приращения координат. Невязки в приращениях по осям координат Для диагонального теодолитного хода формулы
В нашем примере
Вычислив по формуле
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Последнее обновление 15.02.11 19:31 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
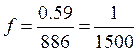
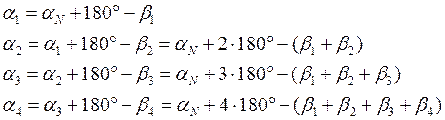
 (1), т.е. дирекционный угол конечной линии равен дирекционному углу начальной (исходной) линии плюс
(1), т.е. дирекционный угол конечной линии равен дирекционному углу начальной (исходной) линии плюс 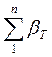 и исходя из равенства, получим для правых углов
и исходя из равенства, получим для правых углов 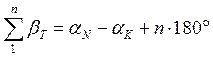 (2). Если вместо правых
(2). Если вместо правых 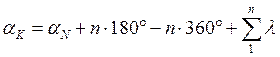 или
или 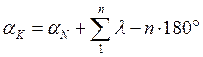 (3).
(3).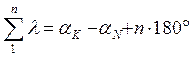 (4).
(4).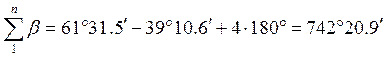 ,
,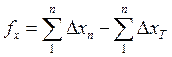 ;
; 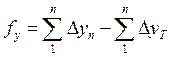 , но число линий хода берут на одну меньше (обьяснить по таблице).
, но число линий хода берут на одну меньше (обьяснить по таблице).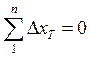
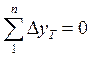 , непригодны, т.к. мы не возвращаемся в ту же точку. Из нашего рисунка видно, что теоретически алгебраическая сумма приращений координат в диагональном ходе по каждой оси равна разности координат исходных конечной и начальной точек хода
, непригодны, т.к. мы не возвращаемся в ту же точку. Из нашего рисунка видно, что теоретически алгебраическая сумма приращений координат в диагональном ходе по каждой оси равна разности координат исходных конечной и начальной точек хода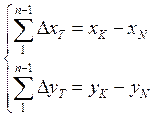
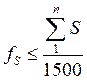 .
.


