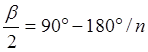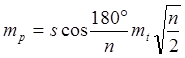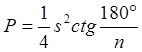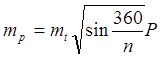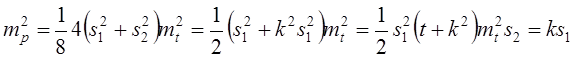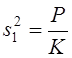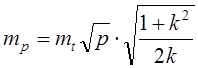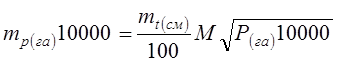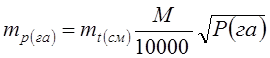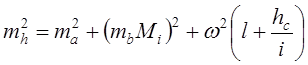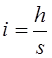| Полный конспект лекций по Инженерной геодезии 25 лекций |
 |
 |
| Добавил(а) Administrator |
| 15.02.11 19:49 |
|
Страница 7 из 38
По этим формулам можно определить ср.кв погрешность площади фигуры любой формы. На практике применяют рабочие формулы для правильных геометрических фигур (прямоугольник, трапеция и т.д.)
Если участок по форме близок к правильному многоугольнику, тогда и
Для фигуры прямоугольной формы с четырьмя точками поворота и соотношением сторон 1 : К при
Для фигуры близкой по форме к квадрату, при n = 4 и К = 1
Чтобы этим формулам придать вид, удобный для расчета точности определения площадей на планах разных масштабов, выразим величины этих формул в метрах, например:
Сравнение этих формул показывает, что погрешности площадей фигур значительно уменьшается с увеличением числа точек фигуры и не сильно увеличиваются с возрастанием коэффициента удлиненности К. Практическая работа № 2. Дать задание по определению ср. грешностей положения на плане точки, расстояния , угла и площади. Лекция 4 Характеристика планово-картографического материала (окончание) 1. Точность превышений и уклонов, определяемых по месту. 2. Искажение линий и площадей в проекции Гаусса-Крюгера. 3. Деформация плана и ее учет при планометрических работах. 1.Превышения и уклоны линий между точками определяются по плану с горизонталями, изображающими рельеф местности. Точность изображения рельефа на плане обычно характеризуют ср.кв. погрешности высоты точки, лежащей на горизонтали, т.е. ср.кв. погрешности положения горизонтали по высоте. Эта погрешность определяется формулой КОППЕ где а – величина, характеризующая точность определения точки земной поверхности по высоте. Сюда входи: погрешности определения высоты станции и превышения между станцией и пикетом, погрешности из-за влияния топографической шероховатости и неоднородности ската между пикетами (обобщения рельефа); в – величина, характеризующая сдвиг точки в горизонтальной плоскости вследствие погрешностей определения планового положения станции, с которой определяются пикеты, планового положения пикетов, интерполирования горизонталей между пикетами, проведения горизонталей и вычерчивания их тушью; γ - угол на плане местности. На основе формулы (1) определялись величины а и в применительно к различным масштабам планов и условий местности. Профессор Видуев Н.В. предложил формулу для определения ср.кв. погрешности положения горизонтали по высоте в зависимости от сечения рельефа h масштаба плана 1/м и уклона местности і Пример: при Наряду с формулой (2) получила распространение формула вида:
где ma - погрешность определения высоты пикетов на местности при помощи геодезического прибора, mb –
Формула В.Д. Большакова: Где M, hc, i - знаменатель масштаба, сечения рельефа и уклон;
l - среднее расстояние между пикетами. Формула Н.Ф. Винницкого : при
Формула Белорусской СХА (кафедра геодезии)
Если точка находится между горизонталями и ее высота определяется интерполированием, то погрешность высоты точки близка к погрешности положения горизонтали, и следовательно, может быть вычислена по приведенным выше формулам. Ср.квадр. погрешности превышения h между т. 1 и 2 с высотами Н1 и Н2, равного h = Н2 – Н1 можно вычислить по формуле
получим Средне квадратичная погрешность уклона, определяется по горизонталям плана, можно получить, исходя их хорошо известной формулы
|