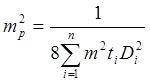| Полный конспект лекций по Инженерной геодезии 25 лекций |
 |
 |
| Добавил(а) Administrator |
| 15.02.11 19:49 |
|
Страница 6 из 38
Если погрешности положения обеих точек равны, что с большей долей вероятности соответствует действительности, т.е. 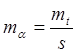 . .
В этих формулах
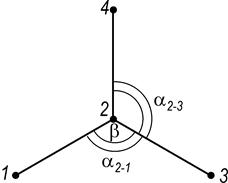
Исходя из этих формул становится понятным, что погрешность дирекционного угла m1= 0,4 мм Погрешность определения направления на плане при помощи транспортира с учетом точности плана получится по формуле Если Еще больше погрешность получится при определении значения угла β по формуле:
Если мы произведем дифференцирование этого выражения, перейдем к ср. квадр. погрешностям и применим формулу:
То получим: C учетом После преобразований получим:
при mt1=mt2=mt3=mt
если
2. Точность площадей контуров, изображаемых на плане. Как и для определения погрешности расстояния и направления на плане, погрешность положения точек контура вызывает погрешность его площади. Как мы знаем, каждая точка на плане определяется независимо от других и характеризуется координатами Хі и Уі со ср. кв. погрешностями mx i и myi. По известной формуле для определения площади по координатам поворотных точек
Можно получить зависимость ср. кв. погрешности площади от координат точек. Продифференцируем это выражение по всем параметрам:
Произведя преобразования и перейдя от дифференциала к ср. кв. погрешности:
учитывая mxi=myi=mk и получим
Из рисунка видно, что выражение в фигурных скобках есть квадраты диагоналей между т. n и 2, 1 и 3, 2 и 4 и т.д. Эти диагонали Dі из теоремы косинусов могут быть выражены через расстояния между точкам і – 1 и і + 1 внутренние углы βі при точках і , следовательно
Тогда
|
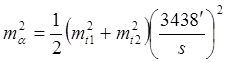 и
и 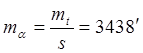
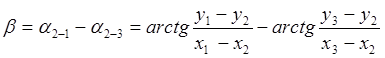
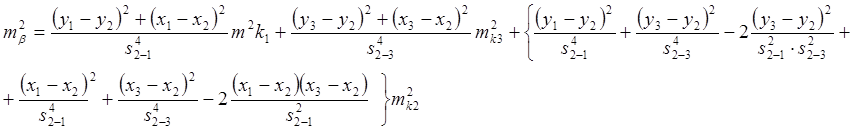
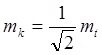 ,
,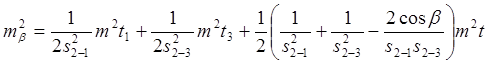
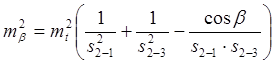 /
/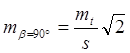 , а при
, а при 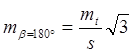 , что значительно превышает погрешность, полученную по формуле:
, что значительно превышает погрешность, полученную по формуле: 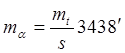
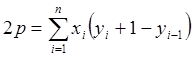
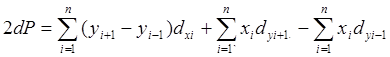
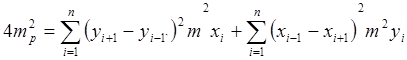
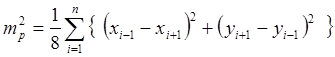 m2t
m2t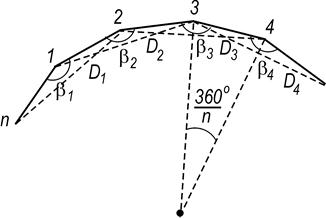
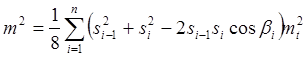 , или
, или