| Полный конспект лекции по топографии 23 лекции. |
 |
 |
| Добавил(а) Administrator |
| 15.02.11 18:53 |
|
Страница 4 из 31
В геодезии наибольшее распространение получали следующие системы координат: географическая (геодезическая и астрономическая), полярная, плоская прямоугольная и зональная. Географическая система. Сюда входят геодезическая и астрономическая системы координат. В геодезической системе за основную координатную повехность, на коотрой определяется плановое положение точек Земли, принимается поверхность референц-эллипсоида, а за основные координатные линии – геодезические меридианы и параллели. Геодезическим меридианом называется сечение эллипсоида плоскостью, проходящей через данную точку и малую (полярную) ось Рс-Рю . В этой плоскости лежат нормали к эллипсоиду в точках меридиана. Геодезической параллелью называется сечение эллисоида плоскостью, проходящей через данную точку и перпендикулярную к малой оси РсР ю. Параллель, проходящая через центр эллипсоида, называется экватором. Положение точки на эллипсоиде определяется пересечением меридиана и параллели, проходящих через данную точку. Меридиан задается геодезической долготой точки, а параллель – геодезической широтой. Геодезической широтой В точки называется угол между нормалью к поверхности эллипсоида в данной точке и плоскостью экватора. Геодезической долготой L точки называется двугранный угол между плоскостью геодезического меридиана данной точки и плоскостью начального (нулевого) меридиана, за который принят меридиан Гринвичской обсерватории в Англии. В астрономической системе координаты определяют относительно направлений отвесных линий в точках земной поверхности. Астрономической широтой Астрономическая долгота Астрономический меридиан – сечение эллипсоида плоскостью, проходящей через отвесную линию в данной точке и параллельную оси вращения Земли. Как следует из определения, астрономические и геодезические координаты различаются на величины, зависящие от несовпадения направлений нормалей к эллипсоиду и отвеса – уклонений отвесных линий, что связано с неравномерным распределением масс в теле Земли, т.е. с гравитационными аномалиями. Различие между астрономическими и геодезическими координатами в среднем составляет Более общее название астрономической и геодезической систем – географическая система координат, которой мы и будем пользоваться, предполагая определение координат геодезическим методом. В этой системе счет долгот ведется от Гринвичского меридиана к востоку (положительная) на Плоские прямоугольные координаты Плоскими прямоугольными координатами называются линейные величины – абсцисса и ордината, определяющие положение точки на плоскости. Систему этих координат представляют две взаимно перпендикулярные линии. Точка их пересечения О называется началом координат, а сами прямые – осями координат. Прямая х-х, совпадающая с направлением меридиана, называется осью иксов или осью абсцисс, а прямая у-у, перпендикулярная к оси абсцисс, - осью игреков или осью ординат(не путать с системой, принятой в математике). В системе прямоугольных координат положение любой точки на плоскости относительно начала координат О определяется кратчайшими расстояниями до нее от осей координат. Так положение точки М определяется длинной перпендикуляров Mp и Mn, опущенных из этой точки на оси координат On и Op. Отрезок On называется абсциссой, а отрезок Op – ординатой точки М. Обозначаются они соответственно х и у и выражаются в линейной мере (обычно в метрах). Оси координат разделяют плоскость чертежа на 4 части, называемые четвертями. Нумерация четвертей I, II, III, IV и направление отсчета углов в этой системе ведется по ходу часовой стрелки, т.е. вправо (не путать с нумерацией в математике, где левая нумерация четвертей). В таблице приведены знаки абсцисс и ординат для точек, находящихся в различных четвертях и даны их названия. Абсциссы точек, расположенных вверх от оси ординат, считаются положительными, вниз – отрицательными. Ординаты точек, расположенных вправо от оси абсцисс, считаются положительными, влево – отрицательными. Положение любой точки местности определяется ее координатами (объяснить на примере нескольких точек в разных четвертях). Полярная система координат При составлении планов и карт небольших участков местности могут быть применены полярные координаты. Положение точки в этой системе определяется относительно некоторой произвольно выбранной исходной точки О, называемой полюсом и полярной осью Ох. Соединив точку N с полюсом О, получим расстояние r, которое называется радиус-вектор и угол Биполярные координаты В этой системе координат два произвольно выбранных неподвижных полюса О1 и О2 соединенные прямой – полярной осью, позволяют определить положение точки М относительно полярной оси на плоскости при помощи двух углов Зональная система координат Из перечисленных выше систем координат, только географическая может быть распространена на всю земную поверхность. Однако использование ее весьма затруднено ввиду сложности решения ряда технических задач на сфере, т.к. географические координаты выражаются в градусной мере, тогда как все расстояния на земной поверхности определяются в метрах. Значительно проще решаются эти задачи в удобной системе плоских прямоугольных координат. Для установления связи между географическими координатами любой точки на сфероиде и прямоугольными координатами этой же точки на плоскости применяют зональную систему координат. Эта система основана на равноугольной (конформной) поперечно-цилиндрической проекции Гаусса и называется системой координат Гаусса-Крюгера. Сущность этой проекции заключается в следующем. 1.Земной эллипсоид меридианами разбивается на шести и трехградусные зоны. Средний меридиан называют осевым. Нумерация зон ведется на восток. Осевые меридианы лежат на внутренней поверхности цилиндра, в котором сферическая поверхность разбивается на отдельные участки(всего 60). 2.Каждая зона в отдельности конфермно проектируется на плоскость таким образом, чтобы осевой меридиан изображался прямой линией без искажений (т.е. с точным сохранением длин вдоль осевого меридиана). Экватор также изобразится прямой линией. За начало счета координат в каждой зоне принимается пересечение изображения осевого меридиана – оси абсциссе х и экватора – оси ординат у. Линии, параллельные осевому меридиану и экватору образуют прямоугольную координатную сетку. 3.Искажения длин линии в проекции Гаусса-Крюгера возрастают по мере удаления от осевого меридиана пропорционально квадрату ординаты. Эти искажения на краях шестиградусной зоны могут достигать величины порядка 1/1500 длины линии, а в трехградусной зоне 1/6000. Для отрезка В съемках крупного масштаба такими искажениями пренебрегать нельзя. В этом случае, при расположении участка на краю зоны, следует или учитывать искажения, или применять частную систему координат с осевым меридианом, проходящим примерно через середину участка работ.
|
| Последнее обновление 15.02.11 19:31 |
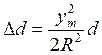 , где
, где 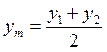 и R- средний радиус кривизны.
и R- средний радиус кривизны.


