| Лекция Постановка и решение задач систем массового обслуживания. Многоканальные системы с отказами |
 |
 |
| Добавил(а) Administrator |
| 18.02.11 17:35 |
|
Страница 1 из 4 Лекция Постановка и решение задач систем массового обслуживания. Многоканальные системы с отказами 12. Постановка и решение задач систем массового обслуживания. Многоканальные системы с отказами Вопросы темы: 1. Многоканальная система с отказами. Задача Эрланга 2. Системы массового обслуживания с ожиданием (очередью) 3. Одноканальная система с неограниченной очередью 4. СМО с ограниченной очередью 12.1 Многоканальная система с отказами Задача Эрланга. Пусть имеется каналов, на которые поступает поток заявок с интенсивностью Система
Поток заявок последовательно переводит из любого левого состояния в соседнее правое с постоянной интенсивностью Для схемы процесса гибели и размножения формулы предельных вероятностей имеют вид:
или с учетом постоянства интенсивности потока
Заменив
В данном виде, формулы предельных вероятностей, называются формулами Эрланга. Показатели эффективности многоканальной СМО с отказами. Вероятность отказа: Относительная пропускная способность системы: Абсолютная пропускная способность системы: Среднее число занятых каналов или математическое ожидание числа занятых каналов: Задача: Заявки на телефонную станцию поступают с интенсивностью 90 заявок в час, средняя продолжительность разговора 2 минуты. определить показатели эффективности работы СМО в случае одного телефонного номера. Определить оптимальное число телефонных номеров, если в качестве показателя эффективности принять относительную пропускную способность системы > 0,90. Решение: Ранее определены показатели эффективности системы для случая одного телефонного номера. Интенсивность потока заявок: Среднее время обслуживания: Интенсивность потока обслуживаний: Относительная пропускная способность системы: В среднем обслуживается 25% из числа поступивших заявок.
|
| Последнее обновление 27.06.18 19:37 |

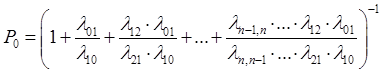
 ,
, 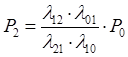 , …,
, …, 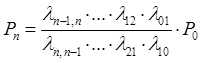
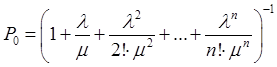
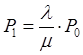 ,
, 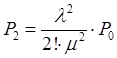 , …,
, …, 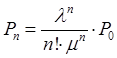
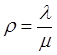 , где
, где 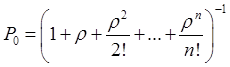
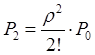 , …,
, …, 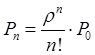
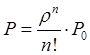
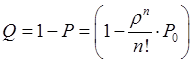
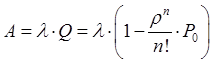
 , где
, где 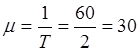 (1/час)
(1/час)