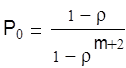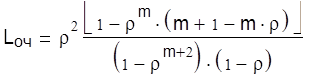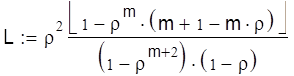| Лекция Постановка и решение задач систем массового обслуживания. Многоканальные системы с отказами |
 |
 |
| Добавил(а) Administrator |
| 18.02.11 17:35 |
|
Страница 3 из 4
Среднее число заявок под обслуживанием определяется по формуле математического ожидания
или среднее число заявок под обслуживанием равно вероятности занятости канала.
Среднее число заявок в очереди
Формулы Литтла. Утверждение: При любом потоке заявок, при любом распределении времени обслуживания, при любой дисциплине обслуживания среднее время пребывания заявки в системе (очереди) равно среднему числу заявок в системе (очереди) деленному на интенсивность потока заявок.
Следствие: В предельном, стационарном режиме, среднее число заявок прибывающих в систему равно среднему числу ее покидающих, или оба потока должны иметь одинаковую интенсивность
Задача: Порт имеет один причал для разгрузки судов. Интенсивность потока 0,4 в сутки, среднее время разгрузки одного судна 2 суток. В предположении неограниченности очереди определить показатели эффективности работы причала и вероятность ожидания разгрузки не более 2 судов. Решение:
Предельные вероятности состояния: - причал свободен - причал занят вероятность ожидания 0,1,2 судов
Вероятность ожидания разгрузки в очереди не более 2 судов
Среднее число судов ожидающих разгрузку
Среднее время ожидания
Среднее число судов в порту
Среднее время пребывания судна
12.4 СМО с ограниченной очередью. В этом случае число заявок в системе не может превышать заданного числа m, заявка поступившая в момент когда все места в очереди заняты покидает систему не обслуженной. В этом случае справедливы формулы для СМО с неограниченной очередью с суммированием для конечного отрезка ряда. Задача: Порт имеет один причал для разгрузки судов. Интенсивность потока 0,4 в сутки, среднее время разгрузки одного судна 2 суток. Определить показатели работы порта при условии, что судно покидает порт при наличии в очереди более 3 судов. Решение: Судно покинет порт без разгрузки, если длина очереди m=3 Предельные вероятности состояния: Причал свободен По условию задачи
Вероятность отказа
Относительная пропускная способность причала
Абсолютная пропускная способность причала
Среднее число судов в очереди под разгрузку
|
| Последнее обновление 27.06.18 19:37 |
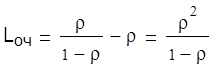
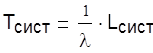
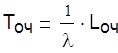
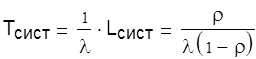
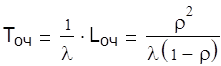

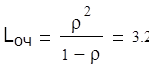
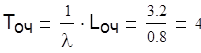 суток
суток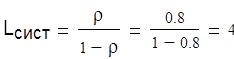 судна
судна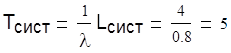 суток
суток