| Про задачі на побудову в шкільному курсі геометріії і форму запису їх розв’язань |
 |
 |
| Добавил(а) Administrator |
| 27.11.11 19:43 |
|
ПРО ЗАДАЧІ НА ПОБУДОВУ В ШКІЛЬНОМУ КУРСІ ГЕОМЕТРІІЇ І ФОРМУ ЗАПИСУ ЇХ РОЗВ’ЯЗАНЬ
Особливе місце у формуванні мислення учнів займає геометрія, яка сприяє розвитку евристичної, тобто творчої його спрямованості, просторової уяви, строгої логіки висловлень з одного боку і пошукової активності, фантазії з іншого. Але це відбувається лише тоді, коли окремі логічні вислови, теореми геометрії сприймаються учнями не як сукупність відокремлених один від одного фактів, а вибудовується в процесі навчання зв’язок між ними, а сама сукупність фактів сприймається як цілісна модель оточуючого світу. Формування вміння аналізувати, узагальнювати, бачити зв’язки, уявити, що відбудеться, якщо змінити умову задачі --- це і є розвиток мислення, творчого потенціалу особистості, здібностей до пошукової діяльності. В свою чергу, в процесі вивчення геометрії особливе місце займають задачі на побудову. Вони важливі при вивчення геометрії, бо вимагають від учня саме діяльності (провести, відкласти, поділити тощо). Розв’язання задач на побудову полегшує початок розвитку просторової уяви, бо аналіз в задачі на побудову --- це міркування в процесі пошуку способів розв’язання, коли учень «робить вигляд», що шукана побудова відбулася. Такі задачі також сприяють формуванню в учнів вміння виділяти окремі кроки в процесі розв’язання та фіксувати їх в процесі його пояснення, бо при розв’язанні задач на побудову такі кроки пов’язані з практичною діяльністю. З іншого боку, задачі на побудову у старших класах сприяють формуванню строгості логічного мислення (відокремлення аналізу умови від саме побудови, а останього від доведення; необхідної умови від достатньої), а їх запис --- вміння обгрунтовано та лаконічно формулювати думку. Нажаль, загальноосвітня школа обминає задачі на побудову. Це пов’язано, мабуть, з тим, що традиційний запис розв’язання цих задач занадто громіздкий. У деталізованому мовному творі-описі всіх рухів циркуля, лінійки та олівця губляться не тільки учні, але й їхні вчителі. Дійсно, тривалий час, аж до змін у змісті екзаменів з математики на атестат про середню освіту та за курс основної школи запис розв’язування задач на іспитах як старшої, так і основної школи, здійснювався надмірно деталізованою мовою і інколи нагадував літературний твір (особливо у “медальних” роботах). Але сьогодні змінився зміст випускних іспитів на атестат про середню освіту, а вимоги щодо запису розв’язаня завдань з математики наближуються до вимог ВНЗ-ів для абітурієнтів. Виникає питання, чи повинен письмовий запис розв’язування задачі обов’язково мати форму твору-опису, тобто повторювати пояснення розв’язування біля дошки або доведення математичних тверджень у підручнику? Мовний опис доведення математичних тверджень у підручнику має на меті полегшити початкове сприйняття навчального матеріалу учнем, дозволити йому ще раз “почути” таке пояснення вдома, надати можливість учню скористатися підручником у випадку пропуску занять у школі. А мета письмового оформлення розв’язання задачі учнем (абітурієнтом) – надати можливість вчителю (екзаменатору) прослідкувати за послідовністю логічних кроків міркувань учня (абітурієнта). Свідченням математичної культури учнів є чітке усвідомлення умови задачі, вміння моделювати розв’язання та виділяти логічні кроки доведень, лаконічність записів розв’язування задач, правильне і раціональне використання позначень та математичної символіки. Відомо, що при обгрунтуванні логічних кроків розв’язання задач як на доведення, так і на обчислення, учні повинні спиратись на опорні факти. Опорні факти — це відомі математичні твердження, співвідношення, які є підставою для логічних висновків. Ними можуть бути: · математичні твердження, що містить теоретичний матеріал шкільного підручника (аксіоми, теореми, ознаки, означення); · базові (опорні) задачі, на які учні в процесі навчання спиралися при розв’язанні складених задач; · відомості, одержані учнями поза шкільною програмою під керівництвом вчителя або самостійно. Чому не скористатися тим самим підходом і при офрмленні розв’язання задач на побудову? Розв’язання задач на побудову та його запис перестане бути каменем спотикання для учнів та вчителів, якщо, після відпрацювання перших опорних задач на побудову з допомогою циркуля та лінійки, надалі розпочинати розв’язання не з засічок циркуля, а з пошуку та виділення цих опорних задач (як то пропонується, наприклад, у [1]). при тому в деталізацію опорних побудов учень при розв’язанні не вдається. Опорними задачами (фактами) геометричних побудов можуть бути: побудова перпендикуляра до заданої прямої, що проходить через задану точку (на даній прямій, або поза нею); кута, що дорівнює даному; знаходження середини відрізка; побудова бісектриси кута; прямої, що паралельна даній прямій і проходить через дану точку; дотичної до кола, що проходить через дану точку (на колі, або поза ним); базових трикутників за: трьома сторонами, двома сторонами і кутом між ними, стороною і двома кутами, двома сторонам і кутом, що не лежить між ними (два розв’язки); базових прямокутних трикутників за: двома катетами, катетом та гіпотенузою, гіпотенузою і гострим кутом; катетом і гострим кутом (два випадки); сегмента, що вміщує даний кут; суми (різниці) відрізків; відрізків, довжина яких дорівнює середньому арифметичному та середньому пропорційному довжин двох заданих відрізків; відрізка, квадрат довжини якого дорівнює сумі (різниці) квадратів двох даних відрізків; відрізка, довжина якого дорівнює добутку довжин двох даних відрізків, поділену на довжину третього та інші. Якщо задачі, перелічені вище, є опорними (тобто їх розв’язання зафіксовано в зошитах і пам’яті учнів, і вони вміють виконувати відповідні побудови та проводити відповідні доведення), то розв’язання і запис розв’язання більш складних задач може спиратись на них, як на “цеглинки”. Розв’язання стає менш громіздким, більш прозорим, полегшується як пошук шляхів розв’язання, так і його запис. Треба зауважити, що Використання опорних фактів при розв’язуванні задач не означає, що в роботі учень може зовсім опустити відповідний логічний крок. Робити відповідне посилання при розв’язанні Обов’язково. Що стосується форми запису, то як Один з варіантів запис логічного кроку розв’язання задачі може мати таку форму: Ліворуч записуються вихідні твердження, праворуч — твердження-висновок; ці блоки сполучаються між собою або словом «тому», або просто умовною стрілочкою «®» (знак слідування «
(Тут те, що Аналогічно, для запису логічного кроку плану побудови при оформленні розв’язування задачі на геометричні побудови, зручно використовувати форму “МАЄМО” f “БУДУЄМО”. Наприклад, логічні кроки ділення відрізка навпіл та побудови прямокутного трикутника за гіпотенузою і катетом можна записати, відповідно, як
Подібна форма запису розв’язання допомагає учням чітко усвідомити структуру логічного кроку, тобто, на що він спирався, коли формулював твердження. Окремі логічні кроки доцільно Ще й Пронумеровувати. – тоді чітко вимальовується модель розв’язання задачі. Така методика запису розв’язання задач в процесі навчання математиці (особливо на перших порах вивчення геометрії) сприяє формуванню в учнів чіткого логічного мислення, вміння «бачити» схему розв’язання, планувати його, аналізувати раціональність певних способів розв’язання і, зрештою, розумінню того, що представляє собою математичне твердження та його доведення. Тоді запис розв’язування задач на побудову може мати наступний вигляд. Приклад 1. Побудувати прямокутний трикутник за гострим кутом і бісектрисою прямого кута.
Побудувати: ПЛан побудови 1) 2) 3) 4)
Доведення За побудовою маємо:
Довести: 1) (3) и (4) виконуються за побудовою. 2) У 3) Приклад 2.Побудувати рівнобедрений трикутник за двома нерівними висотами. Дано:
План побудови 1) 2) 3) 4)
Доведення За побудовою маємо: Довести: АВ = ВС, висоти 1) 2) 3) 4) 5)
Приклад 3. Побудувати трикутник за трьома медіанами.
Побудувати: Аналіз
План побудови1) 2) 3) 4) 5)
ДоведенняЗа побудовою маємо:
Довести: (1); (2); (3).
2)
1. Апостолова Г. В. Планіметрія-7. К.: Генеза, 2004. 2. Апостолова Г. В. Геометрія в опорних схемах і малюнках. Робочий зошит учня 7 класу. К.: Генеза, 2005. 3. Апостолова Г. В., Ясінський В. В. Геометрія старшокласникам і абітурієнтам. |
| Последнее обновление 27.11.11 21:32 |

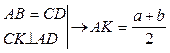 .
. Дано:
Дано:  Побудувати:
Побудувати: 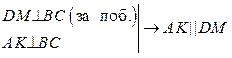 ;
;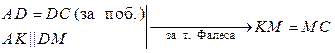 ;
;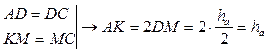 , щ. в. д.
, щ. в. д.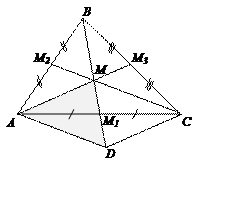 Дано:
Дано: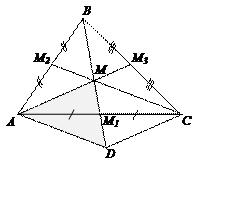 1)
1)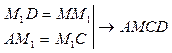 — паралелограм.
— паралелограм.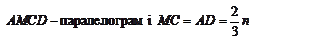 1)
1)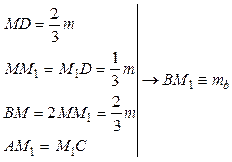 ;
;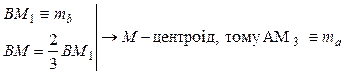 ,
,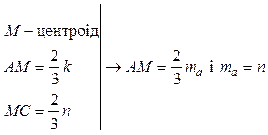 ;
;


