| НА ДОПОМОГУ ВЧИТЕЛЮ, ЯКИЙ ПРАЦЮЄ ЗА ПІДРУЧНИКОМ Галини Апостолової «Геометрія-8» |
 |
 |
| Добавил(а) Administrator | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 27.11.11 19:43 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
НА ДОПОМОГУ ВЧИТЕЛЮ, ЯКИЙ ПРАЦЮЄ ЗА ПІДРУЧНИКОМ Галини Апостолової «Геометрія-8»Вашій увазі пропонуються методичні рекомендації автора підручника щодо роботи з учнями у ІІ семестрі 8-го класу і орієнтовне календарно-тематичного планування навчального матеріалу для класів, що працюють за загальноосвітньою програмою. У квадратних дужках наводять поради щодо викладання відповідного матеріалу у класах з поглибленим вивченням математики та на позакласних заняттях у ЗОШ. Просимо вчителя звернути увагу на Головну мету викладання геометрії в ІІ-му СЕМЕСТРІ 8-ого класу: - Формування в учнів навичок роботи з подібними трикутниками, що є важливою частиною апарату дослідження геометричних фігур і часто застосовується не тільки в геометрії, а й при вивченні суміжних дисциплін; - засвоєння учнями означень і властивостей тригонометричних функцій гострого кута, що є важливим як для засвоєння алгоритмів обчислення прямокутних трикутників так і для подальшого вивчення тригонометрії та суміжних дисциплін; - формування в учнів практичних навичок роботи з вектором, як напрямленим відрізком, що важливо для вивчення фізики і є пропедевтикою подальшого вивчення векторів у 9-му класі. Орієнтовне календарно-тематичне планування навчального матеріалу для класів, що працюють за загальноосвітньою програмою (ІІ семестр – 2 години на тиждень, усього 38 годин) ІІ СЕМЕСТР
Зауваження. Наведене календарно-тематичне планування є орінтовним і може змінюватися залежно від навчального плану конкретного навчального закладу і потреб учнів. МЕТОДИЧНІ РЕКОМЕНДАЦІЇ ЩОДО ВИКЛАДАННЯ ОКРЕМИХ ТЕМ Подібність трикутників - 14 год [21 год]* ДО УРОКУ № 36. Доцільно почати вивчення цієї теми з повторення поняття пропорції, пропорційних величин, відрізків (див. с. 109), можна розглянути історію формування цього поняття (рубрика „Для допитливих” - с. 111). Далі нагадуємо учням теорему Фалеса і формулюємо терему про пропорційні відрізки (узагальнену теорему Фалеса). Можна, запропонувати учням зробити практичну роботу №24 (с. 114) і самостійно сформулювати вказану теорему, після того спитати чи є доведенням теореми здійснена ними робота і чому. Саме доведення цієї теореми для класів ЗОШ можна провести на факультативних заняттях, або запропонувати розібрати його окремим учням (на окрему оцінку) і доповісти на позакласних заняттях. Пропоноване вище дозволить на цьому ж уроці розглянути з учнями доведення оберненої теореми до узагальненої теореми Фалеса, опорну задачу на побудову четвертого пропорційного відрізка (опорна задача №2 на с. 113). [У класах з поглибленим вивченням математики та позакласних заняттях у ЗОШ при вивченні цієї теми, окрім доведення узагальненої теореми Фалеса, пропонується звернути увагу учнів на: опорні задачі №1 і №3 на с. 112 і 113; задачі з двома зірочками на с. 115 та задачі рубрики „Для допитливих” на цій самі сторінці; доведення леми Архімеда про перпендикуляри на січну та розв’язування задач за допомоги цієї леми (рубрика „Для допитливих” на с. 116 і с. 117 відповідно).] ДО УРОКІВ № 37-38. На цьому уроці пропонується (окрім означення подібності трикутників) довести теорему – основну теорему подібності (с. 117). Зауважимо, що доведення цієї теореми значно полегшить у подальшому подання учням ознак подібності, розв’язування задач на подібність. Практичну роботу № 25 можна задати учням як домашнє завдання – це сприятиме закріпленню розуміння й засвоєння вивченого через практичну діяльність. ДО УРОКІВ № 39-40. Завдяки використанню основної теореми подібності доведення перших двох ознак подібності трикутників вміщується у три логічні кроки. Щоб полегшити засвоєння навчального матеріалу з доведення ознак подібності зверніть увагу учнів на те, що спосіб доведення всіх трьох ознак подібності трикутників один і той самий: Відклавши на двох сторонах більшого трикутника відрізки, які дорівнюють відповідним сторонам меншого трикутника, маємо допоміжний трикутник, подібний до більшого з даних трикутників і доводимо його рівність меншому трикутнику. Крім того, виконання практичних робіт №26 - № 28 також тому сприятиме (через практичну діяльність учнів)*. В КОНЕЦ СТР.*Зауважимо, що у випадку „слабкого класу” доцільно пропонувати учням виконання практичної роботи перед формулюванням (доведенням) відповідної теореми. [У класах з поглибленим вивченням математики та позакласних заняттях у ЗОШ зверніть увагу на: задачі відповідних завдань з двома зірочками; задачі рубрики „Для допитливих” на с. 121-123.] ДО УРОКУ 41. Зверніть увагу учнів, що спираючись на вже відомі їм ознаки подібності трикутників можна відразу сформулювати ознаки подібності прямокутних трикутників за пропорційністю обох катетів і за рівністю одного з гострих кутів. Отже залишається довести лише ознаку подібності за пропорційністю одного з катетів і гіпотенузи, яку ми доводимо вже відомим нам методом: Відклавши на двох сторонах більшого трикутника відрізки, які дорівнюють відповідним сторонам-катетам меншого трикутника, маємо допоміжний трикутник, подібний до більшого з даних трикутників і доводимо його рівність меншому трикутнику. Доцільно запропонувати учням Самостійну роботу (на 15-20 хвилин) з метою діагностики рівня засвоєння навчального матеріалу даної теми, скориставшись тестовими завданнями (с. 242-243). ДО УРОКУ 42. Доцільно ще раз повторити з учнями формулювання ознак подібності трикутників, прямокутних трикутників і закріпити навички розв’язування задач на подібність трикутників, виходячи з результатів самостійної роботи, скориставшись задачами завдань 18-21. [У класах з поглибленим вивченням математики та позакласних заняттях у ЗОШ запропонуйте учням софізм рубрики „Для допитливих” зі с. 124; зверніть увагу на задачі рубрики „Для допитливих” - с. 127-129.] ДО УРОКУ 43. Важливо підвести учнів до розуміння (на наочно-інтуітивному рівні), що у подібних трикутниках усі відповідні лінійні елементи пропорційні з одним і тим самим коефіцієнтом пропорційності, який дорівнює коефіцієнту подібності даних трикутників. У цьому вам допоможе формулювання і доведення властивостей подібних трикутників (с.132) та виконання практичних робіт № 30 – 32. [У класах з поглибленим вивченням математики та позакласних заняттях у ЗОШ можна використати задачі з двома зірочками завдання 22 (с. 135) та задачі рубрики „Для допитливих” на с. 139.] ДО УРОКУ 44. Доцільно ще раз повторити з учнями формулювання ознак подібності трикутників, прямокутних трикутників і закріпити навички розв’язування задач на подібність трикутників, скориставшись задачами завдання 22 або практичними задачами, наведеними у § 22. При тому можна запропонувати здійснити певні практичні виміри на місцевості як домашнє завдання. ДО УРОКІВ 45-46. Зауважимо, що теоретичний матеріал відповідного параграфу (§ 23) легше і швидше сприймається й запам’ятовується учнями у вигляді опорних схем (полегшує виділення відповідних пар трикутників). Для того можна використати опорні схеми на полі підручника, або скористатися посібником „Геометрія в опорних схемах. Робочий зошит учня 8 класу”, або скласти (й розмножити) для учнів власні опорні схеми. При розв’язуванні задач зверніть увагу на опорні задачі побудови (опорні задачі 1 і 2 на с. 141 і 142). Наприкінці уроку № 46 пропонуємо провести діагностичну Самостійну роботу (15 хвилин) –орієнтовно задачі № 3-б/№4 і №9а/№9б завдання 23 (с. 143). [У класах з поглибленим вивченням математики та позакласних заняттях у ЗОШ зверніть увагу на доведення узагальненої теореми Піфагора (рубрика „Для допитливих” на с. 140); теорему Евкліда (Додаток 4 на с. 211); можна використати задачі з двома зірочками завдання 23 (с. 143-144) та задачі рубрики „Для допитливих” на с. 140 - 142.] ДО УРОКІВ 47-48. На цих уроках продовжуємо застосовувати властивості подібності до розв’язування задач, зокрема на прикладі задач із колом, з бісектрисою трикутника. Вчитель в залежності від рівня засвоєння учнями навчального матеріалу вирішує який саме матеріал з § 24 й завдання 24 задіяти для роботи з учнями. Можливо треба обмежитися знайомством з теоремами 1-3, без їхніх наслідків. (Вивчення вказаних наслідків запропонувати окремим учням здійснити самостійно.) Зверніть увагу учнів, що використання подібності трикутників, утворених додатковими побудовами (як то, наприклад, ми роблять при доведенні теореми про добуток відрізків хорд кола, що проходять через фіксовану точку в середині кола) називають Методом подібності. [У класах з поглибленим вивченням математики та позакласних заняттях у ЗОШ зверніть увагу на наслідки до теорем 1-3 з § 24; формулу Лагранжа (с. 147) і теорему Птолемея (с.148); опорні задачі №1 і №2 на с. 148 і 149; задачі з двома зірочками завдання 24; доведення леми Архімеда про перпендикулярні хорди й задачі на її використання (рубрика „Для допитливих” на с. 151).] ДО УРОКУ 49. Продовжуємо застосовувати властивості подібності до розв’язування задач, зокрема на прикладі задач із трапецією. Вчитель в залежності від рівня засвоєння учнями навчального матеріалу вирішує який саме матеріал з § 25 й завдання 25 задіяти для роботи з учнями. Можливо треба обмежитися знайомством з опорними задачами № 4 і №5(а-в) і повернутися до розв’язування задач попередніх завдань або використати завдання для повторення розділу ІІІ (с. 156). [У класах з поглибленим вивченням математики та позакласних заняттях у ЗОШ можна розібрати опорні задачі №1-2 (с. 152); використати задачі № 3, № 5-11 з завдання 25 та задачі рубрики „Для допитливих” на с. 152-154.] ДО УРОКІВ 50-53. Систематизацію й узагальнення знань теми допоможуть провести питання №1-10 завдання на с. 156 та задачі з цього завдання. Доцільно до підсумкової атестаційної роботи (орієнтовне завдання на с. 159) провести 1-2 самостійних роботи на 15-20 хвилин ( орієнтовно за задачами №8 -15 вправ для повторення в тестовій формі на с.244). На підсумковому уроці (урок 53) важливо розібрати з учнями розв’язування задач обох варіантів тематичного оцінювання, ще раз повторити опорні факти теми. Можна запропонувати деяким учнями певні завдання з корекції знань, а окремим учням – завдання підвищеної складності для самостійної роботи (для того можна використати на тільки задачі з завдань розділу, а й задачі у тестовій формі розділу „Перевір себе” с. 242-244). [У класах з поглибленим вивченням математики та позакласних заняттях у ЗОШ можна використати задачі рубрики „Для допитливих” на с. 160.] Розв’Язування прямокутних трикутників – 11 год [14 год] ДО УРОКУ 54. На цьому уроці, уроці вступу до тригонометрії, бажано сформувати в учнів уявлення про важливість її використання у житті людства, історію виникнення її понять. У цьому вам допоможе матеріал § 26, рубрики „Для допитливих” на с. 163, матеріал на полі с.165. Засвоїти відповідність між відношеннями сторін і мірою гострих кутів у прямокутному трикутнику учням допоможе практична робота № 33. Полегшить запам’ятати означення синуса, косинуса, тангенса і котангенса гострого кута опорна схема на полі с. 162 підручника (або відповідна схема у „Робочому зошиті”) – запропонуйте учнями навести різним кольором сторони прямокутного трикутника і відповідними кольорами зафарбувати чисельники і знаменники наведених записів схеми. [У класах з поглибленим вивченням математики та позакласних заняттях у ЗОШ можна використати задачі № 11-13 з завдання 26 (с. 164).] ДО УРОКУ 55. Побудова кута за його тригонометричними функціями дозволить учнями повторити й закріпити означення тригонометричних функцій гострого кута; перейти до ілюстрації значення цих функцій через чверть одиничного кола; зрозуміти зміну значень тригонометричних функцій на інтервалі [0o;90o]. Для того важливою є саме практична діяльність учнів. Тому зверніть увагу на практичні роботи 34-36, задачі №1-4 і №6 з завдання 27. [У класах з поглибленим вивченням математики та позакласних заняттях у ЗОШ можна використати задачі № 5, 7-9 з завдання 27 (с. 167).] ДО УРОКУ 56. Продовжуємо працювати з тригонометричними функціями гострого кута –знайомимо учнів із властивістю тригонометричних функцій гострого кута і кута, що доповнює даний до 90о. Доречно провести Самостійну роботу (на 10 хвилин) за тестовими завданнями № 1-2 на с. 244. [У класах з поглибленим вивченням математики та позакласних заняттях у ЗОШ можна використати задачі рубрики „Для допитливих” на с. 168-169; задачу №7 з завдання 28 (с. 168).] ДО УРОКУ 57. Головна мета уроку № 57 – сформувати в учнів уявлення про те, що основна тригонометрична тотожність є тригонометричним еквівалентом теореми Піфагора, тобто можна сказати, що вся тригонометрія має за свій виток теорему Піфагора. Тоді учням буде легше запам’ятати основну тригонометричну тотожність ДО УРОКУ 58. Формуємо перші навички перетворення тригонометричних виразів. На початку уроку доцільно запропонувати учнями самостійну роботу (5 хвилин) за тестовим завданням № 5 на с.245. При розв’язуванні задач № 3-4 завдання 29 зверніть увагу учнів, на таке.
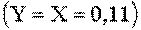 ), то значення ), то значення (Вказане вище є пропедевтикою успішного формування в учнів у майбутньому Навичок роботи з тригонометричними функціями при вивченні тригонометрії.) [У класах з поглибленим вивченням математики та позакласних заняттях у ЗОШ можна використати задачі №7-8 з завдання 29 (с. 170); задачі рубрики „Для допитливих” на с.170.] ДО УРОКУ 59. Щоб встигнути опрацювати з учнями задачі завдання №30, доцільно пояснення здійснювати за готовим кресленням (див. „Робочий зошит”), щоб учні не переписували відповідний матеріал з дошки. Зверніть увагу учнів на те, що табличку значень тригонометричних функцій кутів міри 30о, 45о і 60о легко запам’ятати, якщо скористатися мнємонічним правилом пропонованим на с. 172. [У класах з поглибленим вивченням математики та позакласних заняттях у ЗОШ зверніть увагу на обчислення значення синуса кута міри 18о (с. 172) за допомоги властивостей рівнобедреного трикутника із кутом при вернені у 36о.] ДО УРОКІВ 60-61. Ці уроки пропонуємо присвятити розв’язуванню прямокутних трикутників (§31), у тому числі й у прикладних задачах (§32). Радимо звернути увагу на те, щоб учні не тільки вміли записати значення тригонометричної функції гострого кута прямокутного трикутника через його сторони, але й вміли записувати (без допоміжних перетворень) довжини катетів й гіпотенузи трикутника через тригонометричні функції його гострих кутів й довжину іншої з сторін цього трикутника (поле на с. 174). Приклади з використанням таблиці тригонометричних функцій (с.175-176) можна (за бажанням вчителя) розібрати у класі, можна опустити, можна запропонувати для домашнього опрацювання, бо зараз є обчислювальна техніка, скориставшись якою легко обчислити значення тригонометричних функцій гострих кутів. Проте, радимо не опускати правила роботи з наближеними числами (с.177), бо правильно здійснювати такі обчислення необхідно не тільки у абстрактних математичних завданнях (у тому числі і зовнішнього оцінювання), але й при розв’язуванні прикладних задач, задач у курсі фізики тощо. Зауважимо, що під час літньої практики доцільно здійснити відповідні практичні роботи з задачами §32 на місцевості. Таке не тільки сприятиме закріпленню навичок роботи з тригонометричними функціями, але й підсиленню мотивації навчання математиці. ДО УРОКІВ 62-64. Для узагальнення й систематизувати знань учнів з даної теми можна використати питання та задачі з „Завдання для повторення розділу ІV” (с.183-184). Перед тематичною атестацією (орієнтовне завдання див. на с. 184) доцільно провести діагностичні самостійні роботи (на 5 хвилин і 20 хвилин) за тестовими завданнями № 3 і №6-10 відповідно. Вектор як напрямлений відрізок площини – 3 год [5 год] ДО УРОКІВ 65-67. Дана тема є необов’язковою для вивчення у 8 класі. Проте, радимо присвятити їй трохи часу для ознайомлення з поняттям вектора як напрямленого відрізка, для практичного опрацювання цієї теми (за пропонованими практичними роботами № 37-43 розділу V). Це полегшить засвоєння теми „Вектор на площині” у 9 класі, дозволить використати набуті учнями уявлення і навички на уроках фізики, що, в свою чергу, також потім сприятиме вивченню цієї теми у курсі математики 9-го класу, полегшить застосування учнями векторного методу до розв’язування геометричних задач. Зауважимо, що:
Систематизація і узагальнення навчального матеріалу ДО УРОКІВ 68-70. Для систематизації й узагальнення знань учнів з курсу геометрії 7-8 кл. можна використати завдання для повторення наведені наприкінці вступу до кожного з розділів; опорні конспекти, наведені наприкінці підручника (с. 250-256); схеми на форзацах і полях підручника; завдання в тестовій формі „Перевір себе”. Для формування завдання підсумкової атестації можна орієнтуватися на елементи пропонованих завдань тематичних атестацій №1-4, можна, окрім того, використати й певні тестові завдання розділу „Перевір себе”. На закінчення зауважимо, що підручник містить розділ VI „Цікаві додатки”, матеріал якого можна використати для роботи в класах з поглибленим вивченням математики, на позакласних заняттях, для підготовки учнями реферативних робіт, або робіт у системі МАН. Для останнього можна задіяти задачі та список додаткової літератури, що наведені наприкінці кожного з додатків. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Последнее обновление 27.11.11 21:21 |

 ,
, 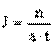 .
.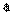 .
.


